2022. 9. 26. 00:00ㆍFunctional Programming/Category Theory
참고 : https://bartoszmilewski.com/2014/11/04/category-the-essence-of-composition/
Category 는 개체와 개체 사이를 이동하는 화살표로 구성된다.
Category 의 본질은 Composition 이다.
객체 A 에서 B 로의 화살표와 객체 B 에서 객체 C 로의 화살표가 있는 경우
A 에서 C 로 가는 화살표 (Composition) 가 있어야 한다.

함수로 표현해보자
(완전한 구현이 아닌 일종의 sudo code 라고 생각하자)
B f(A a); // A 를 입력받아 B 를 return 하는 함수
C g(B b); // B 를 입력받아 C 를 return 하는 함수
위와 같은 함수를 Composition 하면 다음과 같다.
C g_f(A a) => g(f(a)); // A 를 입력받아 C를 return 하는 함수 (Composition g,f)
Haskell 을 통해 구현해 보자
f:: A -> B -- A 를 입력받아 B 를 return 하는 함수
g:: B -> C -- B 를 입력받아 C 를 return 하는 함수
g . f -- A 를 입력받아 C 를 return 하는 함수 (Composition g,f)
Composition의 속성
1. Associative (연관, 결합법칙)
수학에서 결합법칙은 이항연산이 가질 수 있는 성질이다. 한 식에서 연산이 두 번 이상 연속될 때, 앞쪽의 연산을 먼저 계산한 값과 뒤쪽의 연산을 먼저 계산한 결과가 항상 같을 경우 그 연산은 결합법칙을 만족한다고 한다. 실수의 덧셈과 곱셈은 결합법칙을 만족한다. 위키백과
즉 어떤 함수 h, g, f 가 있다고 했을때
f:: A -> B
g:: B -> C
h:: C -> D
h . (g . f) == (h . g) . f == h . g . f즉 함수의 실행에 대한 우선순위가 바뀌어도 그 결과는 항상 같다는 것을 말한다.
2. Identity (동일성)
연산하고 나서 자기 자신이 그대로 return 되는 값
덧셈에서 항등원 은 0 이다.
0+1 == 1+0 == 0+0+1+0+0 == 1
함수로 표현하면 다음과 같다.
C#
public T Identity(T x) => xC++
template<class T> T id(T x) { return x; }Haskel
id :: a -> a
id x = x구현은 모든 형식에 대해 동일 해야 한다.
결과적으로 객체지향형 언어들에서는 Generic 또는 Template 이라고 부르는 것을 통해 처리 가능 하다.
동일성 조건은 다음과 같다.
f . id == f
id . f == f그렇다면 이러한 아무것도 하지 않는 function 에 어떤 장점이 있을까?
나중에 알아볼 Higher order function 의 paramter 로 사용하거나 return 으로 이용할 수 있다.
요약하자면: Category 는 개체와 화살표(함수)로 Composition 된다.
함수는 Composition 될 수 있으며 Composition은 연관(Associative)된다.
모든 개체에는 Composition에서 단위(Unit or Identity) 역할을 하는 ID 함수가 있다.
** 화살표는 morphism 이라고 되어 있지만 morphism 이란 수학에서 사상이라고 해석되며
수학적 구조를 보존하는 함수의 개념을 추상화한 것 이 사상이므로 함수라고 지칭하였다. **
Composition (구성,합성) 은 프로그래밍의 핵심이다.
우리는 더 큰 문제를 더 작은 문제로 분해한다.
더 작은 문제가 여전히 너무 크면 더 분해한다.
마지막으로 모든 작은 문제를 해결하는 코드를 작성한다.
그리고 나서 프로그래밍의 본질이 나온다.
우리는 더 큰 문제에 대한 솔루션을 만들기 위해 이러한 코드 조각을 Composition한다.
각 조각을 다시 모을 수 없다면 분해는 의미가 없다.
Category theory 의 대상은 추상적이고 모호한 개체이다.
그것에 대해 알 수 있는 것은 다른 개체와 어떻게 관련되어 있는지,
즉 화살표(Composition Function)를 사용하여 개체와 연결하는 방법뿐이다.
인터넷 검색 엔진이 들어오는 링크와 나가는 링크를 분석하여 사이트의 순위를 매기는 방식이다.
객체 지향 프로그래밍에서 이상적인 객체는 화살표 역할을 하는 메서드와 함께 추상 인터페이스(순수한 표면, 볼륨 없음)를 통해서만 볼 수 있다. 다른 객체와 구성하는 방법을 이해하기 위해 객체의 구현을 파헤쳐야 하는 순간 프로그래밍 패러다임의 이점을 잃게 된다.
과제
1. 가능한 한 가장 좋아하는 언어(Haskell 제외)로 식별 기능을 구현해보자.
2. 선호하는 언어로 Composition 을 구현해보자
두 개의 함수를 인수로 취하고 그 Compositon 인 함수를 반환해보자.
3. Composition 함수가 동일성을 존중하는지 테스트하는 프로그램을 작성해보자.
1. 구현
public record class Number(int Value)
{
public Number Add(Number number) => number with { Value = Value + number.Value };
public Number Mul(Number number) => number with { Value = Value * number.Value };
public static Number Add(Number x, Number y) => new Number(x.Value + y.Value);
public static Number Mul(Number x, Number y) => new Number(x.Value * y.Value);
private static Number _addIdentity;
public static Number AddIdentity
{
get
{
_addIdentity ??= new Number(0);
return _addIdentity;
}
}
private static Number _mulIdentity;
public static Number MulIdentity
{
get
{
_mulIdentity ??= new Number(1);
return _mulIdentity;
}
}
public void PrintString() => Console.WriteLine(this.Value);
}public void Test()
{
var number1 = new Number(1);
var number2 = new Number(2);
var number3 = new Number(3);
// 1 + 0
number1.Add(Number.AddIdentity).PrintString();
// 0 + 1
Number.AddIdentity.Add(number1).PrintString();
// 1 + 0 == 0 + 1
var addEqual = number1.Add(Number.AddIdentity) == Number.AddIdentity.Add(number1);
Console.WriteLine(addEqual);
// 2 * 1
number2.Mul(Number.MulIdentity).PrintString();
// 1 * 2
Number.MulIdentity.Mul(number2).PrintString();
// 2 * 1 == 1 * 2
var mulEqual = number2.Mul(Number.MulIdentity) == Number.MulIdentity.Mul(number2);
Console.WriteLine(mulEqual);
// (1 + (2 + 3)) + 0
Number.Add(number1, Number.Add(number2, number3)).Add(Number.AddIdentity).PrintString();
// 0 + ((1 + 2) + 3)
Number.Add(Number.AddIdentity.Add(Number.Add(number1, number2)), number3).PrintString();
// (1 + (2 + 3)) + 0 == 0 + ((1 + 2) + 3)
var add2Equal = Number.Add(number1, Number.Add(number2, number3)).Add(Number.AddIdentity) == Number.Add(Number.AddIdentity.Add(Number.Add(number1, number2)), number3);
Console.WriteLine(add2Equal);
}
Extension Method 를 통한 int add 에 대한 identity 구현
public static class IntExtensions
{
public static int Add(this int self, int value) => self + value;
public static int Mul(this int self, int value) => self * value;
//public static int GetAddIdentity(this int self) => AddIdentity;
public static int AddIdentity => 0;
//public static int GetMulIdentity(this int self) => MulIdentity;
public static int MulIdentity => 1;
}
public class IdentityTest2
{
public void Test()
{
// 0 + 1 + 2 + 3
var prefix = IntExtensions.AddIdentity.Add(1).Add(2).Add(3);
// 1 + 2 + 3 + 0
var postfix = 1.Add(2).Add(3).Add(IntExtensions.AddIdentity);
Console.WriteLine(prefix == postfix);
}
}
Composition
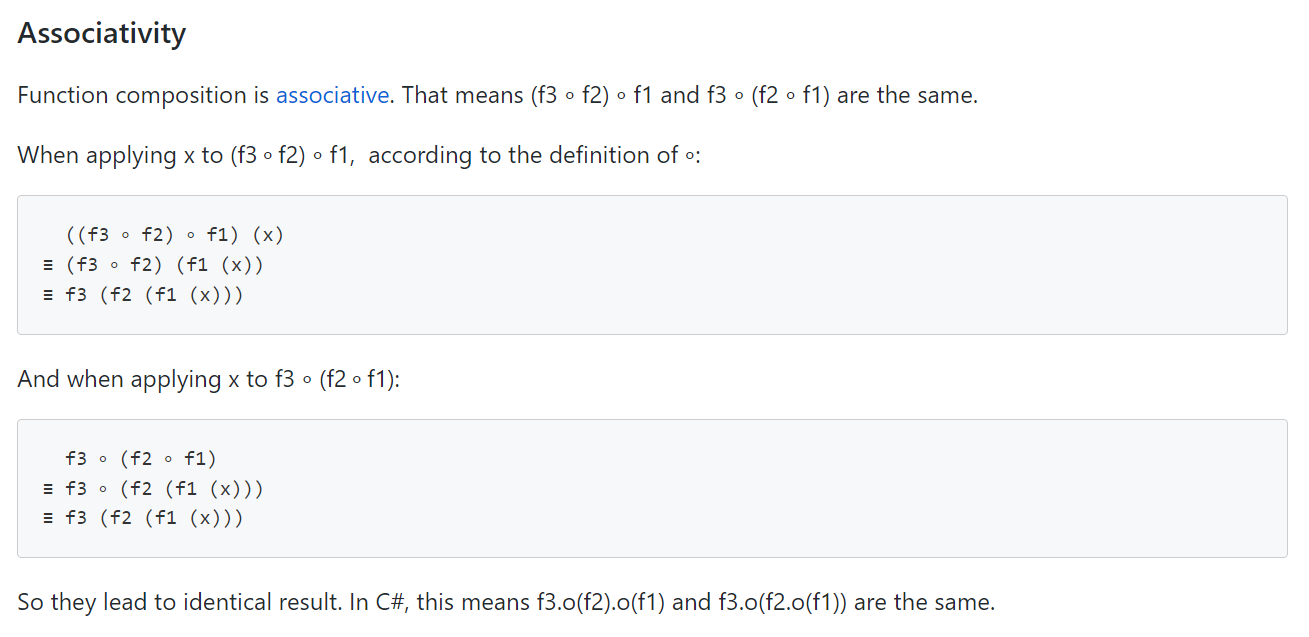
c# 에서 Composition 에서 associativity 란 무엇인가?
2. 구현
public static class CompositionExtension
{
public static Func<T1, T3> Compose<T1, T2, T3>
(this Func<T2, T3> f, Func<T1, T2> g)
{
return x => f(g(x));
}
}
var k = new Func<IEnumerable<string>, string>(s => string.Join(" ", s));
var f = new Func<string, IEnumerable<string>>(s=>s.Split(new[] { ' ' }));
var g = new Func<string, string>(s => s.ToUpper());
var h = k.Compose(f).Compose(g);
Console.WriteLine(h("foo bar") == k(f(g("foo bar"))));
// k.Compose(f).Compose(g) == k(f(g(...)))
// This is the associativity in the meaning of the composition (c# function composition).
3. 구현 (Composition 함수가 identity 를 만족하는지 확인)
public static partial class CompositionExtension
{
public static Func<T1, T3> Compose<T1, T2, T3>
(this Func<T2, T3> f, Func<T1, T2> g)
{
return x => f(g(x));
}
public static T1 Identity<T1>(this T1 x) => x;
}
var f = new Func<int, int>(x => x * x);
var h = f.Compose(f.Identity());
var i = f.Identity().Compose(f);
Console.WriteLine(h(3) == i(3));
관련영상
'Functional Programming > Category Theory' 카테고리의 다른 글
| Product and CoProduct (0) | 2022.10.24 |
|---|---|
| Kleisli Catogories (0) | 2022.10.17 |
| Monoid as Category (0) | 2022.10.10 |
| Types and Functions (0) | 2022.10.03 |
| 잠시 멈추어서... (0) | 2022.09.26 |