2022. 10. 10. 00:00ㆍFunctional Programming/Category Theory
Category 는 여러가지 종류가 있고 그것은 모양과 크기로 나타난다.
No Objects
개체가 없고 결과적으로 모피즘이 없는 범주
Simple Graphs
노드 상에서 가능한 모든 화살표를 그리는 것

Orders (순서, 정렬)
a <=b 이고 b <=c 이면 a <= c 작다 (Composition)
이것들도 category (범주) 라고 할 수 있을까?
일단 composition 은 가능한 걸로 확인되었으니
실제 연관 (Associative) 되었는지 확인 하자.
a<=b , b<=c 는 어느것을 먼저 처리해도 결과 적으로 a <= c 라는 결과를 가져온다.
그러므로 연관되어 있다.
Identity 를 가지고 있는가?
모든 객체는 자신보다 작거나 같다로 표현 가능 하다.
a <= a 가 성립한다 b <=b 가 성립한다. 즉 Identity 를 갖는다.
이와 같은 관계를 갖는 집합을 preorder 라 하고 preorder 는 범주이다.
preorder 은 개체에서 개체로 이동하는 최대 하나의 arrow 가 있는 범주다.
이러한 범주의 또 다른 이름은 Thin Category 이다.
Monoid as Set
- value 들의 집합
- 이진연산 (연관되어 있어야 하고)
- Identity 요소

0 인 자연수는 덧셈에서 모노이드를 형성한다.
Type 은 자연수 이고
덧셈은 이진연산이며
덧셈에서 연관은 아래와 같은 의미 이다.
(a + b) + c = a + (b + c)덧셈에서 Identity 는 다음과 같다.
0 + a = a = a + 0그림으로 표현한다면 다음과 같다.

문자열 concat 같은 경우도 같은 형태로 모노이드를 형성한다.
단 문자열 같은 경우 Identity 는 0 이 아닌 빈 문자열 "" 이 된다.
Monoid as Category
하나의 객체와 그 단일 객체에서 그 자체로 되돌아가는 (엔도-)펑터가 있는 범주이다.
단일 개체 Category 에서 항상 집합을 추출할 수 있고 이 집합은 모피즘의 집합이다.
그래서 항상 Category monoid 에서 Set monoid 를 만들어 낼수 있고 이 둘은 동일하다.
단일 객체만 있는 범주(Category)의 속성은 Monoid 의 정의에 있는 속성과 정확히 동일하기 때문에
단일 객체를 포함하는 범주는 monoid 라고 할 수 있다.


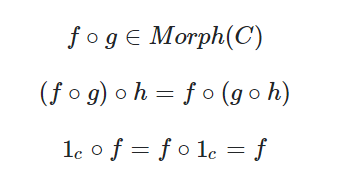
두 (monoid 와 하나의 객체를 갖는 Category)속성은 완전히 동일하다
하나의 객체와 여러개의 화살표가 있는 범주를 모노이드라고 한다.

관련영상
'Functional Programming > Category Theory' 카테고리의 다른 글
| Product and CoProduct (0) | 2022.10.24 |
|---|---|
| Kleisli Catogories (0) | 2022.10.17 |
| Types and Functions (0) | 2022.10.03 |
| Category : The Essence of Composition (Category: Composition 의 본질) (0) | 2022.09.26 |
| 잠시 멈추어서... (0) | 2022.09.26 |